Benford’s law, also called the First-Digit Law, refers to the frequency distribution of digits in many (but not all) real-life sources of data. In this distribution, 1 occurs as the leading digit about 30% of the time, while larger digits occur in that position less frequently: 9 as the first digit less than 5% of the time.

Benford’s law also concerns the expected distribution for digits beyond the first, which approach a uniform distribution.
It has been shown that this result applies to a wide variety of data sets, including electricity bills, street addresses, stock prices, population numbers, death rates, lengths of rivers, physical and mathematical constants,[1] and processes described by power laws (which are very common in nature). It tends to be most accurate when values are distributed across multiple orders of magnitude.
So, does it apply to energy data? Well I ran a little SQL query on 150 million records of 15-minute energy data I had lying around. Here is the distribution of the digits:
“1” 49647887
“2” 27419091
“3” 18099660
“4” 14904116
“5” 13496329
“6” 10929017
“7” 9671925
“8” 7708455
“9” 6564295
and here is the distribution chart:
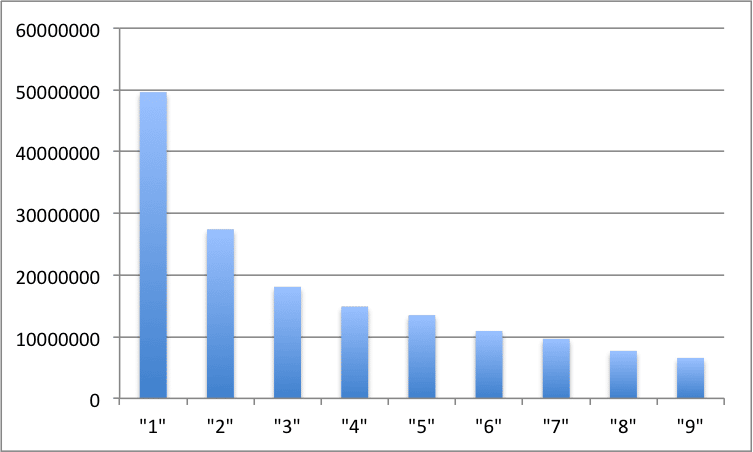
The vast majority of the data analysed are electricity usage data measured in watt hours. However, there are also gas and water usage data in there also. I left out negative numbers for simplicity (negative numbers can legitimately occur when energy is being produced, i.e. exported).
So yes! Benfords law is alive and well in 15 minute energy data. But why does that matter? In the case of our energy data, it demonstrates its veracity and the effectiveness of our data acquisition and data management on a large scale….and its just kind of interesting.