Whilst working on modelling situations in the real world, or thinking about to how tackle a specific problem, it’s often surprising how many things I take for granted. Sometimes it’s worthwhile to consider how seemingly obvious, or ‘given’ information, is actually derived.
The derivation process itself can often shed light and offer further intuition into much harder and/or complex problems.
Lately, I was working on solving a set of equations and becoming lost in a sea of inequalities and variables. Standing back for a moment and writing them out plainly on a whiteboard I realised that what I was in fact looking at was a problem that could be approached and solved quickly using fairly simple geometry rather than complex algebra. It really was a case of I couldn’t see the forest for the trees.
Geometry, in my opinion, is one of the most fascinating and often underappreciated fields of mathematics . I’d like to give you an example of something quite simple and very geometrical which has far reaching consequences in that it contributes to something that you most likely take for granted and also contributes to the fundamental understanding of one of the most important fields of mathematics.
The Area of a Circle
If you’ve made your way through basic geometry I can most likely guarantee that you know that the area of a circle can be calculated with the formula
Area = πr2
But, have you ever wondered why?
Let’s try and work it out.
How about a simple approach, enclosing the circle in a bounding square where the height and width equal the diameter of the circle.
Along with set theory. Set theory is cool.
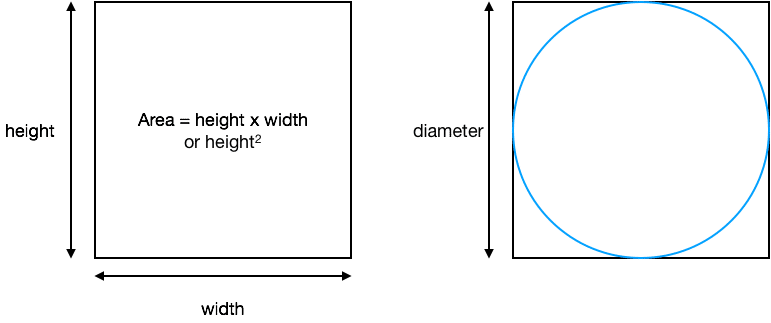
Looks like a good start, but we have 4 sections left over – one at each corner – so the area of the circle would seem to be less than the area of the square. But we can say that,
Areacircle < diameter2
We have a square in there at least. Perhaps we could divide up the circle such that we can calculate the sum of the areas of the smaller parts?
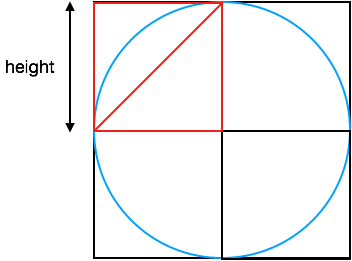
How about if we divide up the circle into quarters, then calculate the area of one of the quarters and multiply by 4?
So, for the triangle in red we would have an.
Areatriangle = ½ * height * height
= ½ height2 * 4
= 2 * height2
Now remember that height is actually the radius of the circle so replacing height for 4 we can write the following inequality for the area of the circle as we’re missing the 4 sections of the circle from the area calculated.
Areacircle > 2 * r2
If only there were some way we could divide up the circle that allowed us to sum it.
Well, how about if we cut it into strips. Concentric strips like this,

Each of the strips divides up the circle into a series of trapezoids, which mathematically are similar to rectangles if we don’t look at them too closely. Bear with me.
Let’s consider just one of them in detail (as the principle can be applied to all of the others that make up the whole covering of the circle).

Although I’ve exaggerated it here for emphasis, the two tapering ends of the rectangle-like shape are actually very small compared with the whole shape – the section labelled width is much bigger in most cases in terms of area than the two ends that consist of triangles.
As we know the formulate for the area of a rectangle its area is very easy to calculate.
Thinking carefully, we know that the width here is approximately equal to the circumference of the circle which is given by the formula
Circumferencecircle = 2 * π * r
The height of the shape is a tricky thing though. Obviously the smaller we make this then the more accurate our measurement will be as the two triangular areas at either end of the rectangle like shape become less significant.
Let’s call this dr for the moment (those of you who’re familiar with calculus might get an inkling as to where I’m heading.)
Now the area of the shape can be said to be, approximately,
Circumferencecircle = 2 * π * dr
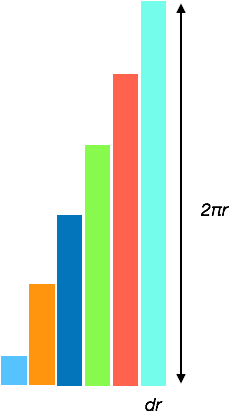
Step back for a second now. We’ve divided up the area of the original circle into the sum of the area of the smaller rectangle like shapes. Considering each rectangle, let’s line them up side by side, staring at the one nearest the centre of the circle.
I’ve made the ends of the rectangle like shapes quite small now so you can’t quite see them.
Each rectangle like shape has an area of
Area = 2 π dr
If we put some axis on this diagram, the x-axis is actually the radius and the y-axis, area.
Let me show this again, a little more clearly, but I’m also going to overlay the graph of
y = 2 π dr
The thing to node is that the rectangle like shapes all barely just touch the line of y = 2 πr.
And also, and more importantly, the smaller that dr becomes the smaller the gaps become between the shapes and the line y = 2 πr.
Remembering that the area of the circle is just the sum of the areas of all of the shapes it’s actually very easy to calculate as the shapes considered together form a simple right angled triangle where the x-axis length is the radius and the y-axis length is 2 πr.
So, the area of the triangle is,
y = 1/2 * x * y
= 1/2 * r * 2πr
= πr2
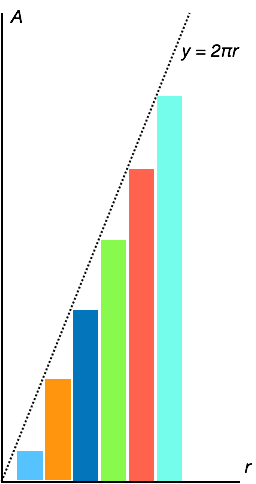
Conclusion
Just reflect on what we’ve done for a moment. It’s pretty cool.
We divided up a circle into a series of concentric rings, laid them out side by side, summed up their areas, and derived a formula for the area of the circle.
As the width of the strips gets smaller (and closer to zero) the area of the triangles on the ends get less significant and the total area becomes a simple width x height.
The point here is that we have taken one large problem (calculating the area of a circle) and split it into a number of smaller problems – each of which in themselves are easy to solve.
Many larger problems can be broken down like this, indeed many larger problems can be reduced to simply calculating the areas under graphs. This was a simple case involving a triangle formed by a straight line equation, but this all should be sounding familiar especially when I tell you that the area under graph is known as the integral of the function that defines it. Yes, it’s in the realm of calculus.
Extra Credit
We did assume that we knew the circumference of a circle is 2 πr in order to derive the formula, but there’s an equally simple and elegant proof for that too, which I’ll leave for your investigation.
Keywords:
Problem, Limits, Sums, Calculus, Circle, Geometry, Reduction, Equation, Integral